Aareyan Manzoor

I am a grad student at Waterloo. My current interests are in the intersection of operator algebras and quantum information. I am a former bangladeshi but current ontorian, and I am a member of the LGBTQ+ community

31 Oct 2021 -

Galois theory in its vanilla form gives us a connection between field theory and group theory. Specifically, for nice field extensions (so called Galois extensions), you can associate to it the group of its automorphisms (the Galois group). Galois theory claims that sub-extensions correspond to subgroups of the Galois group. Now a natural question is, can we say that each finite group \( G\) is the galois group over some extension of a given field? For \( \mathbb{Q}\) , the problem is still open. However for the field \( \mathbb{C}(t)\) , the answer is positive! The proof requires some Riemann surface theory and some covering space theory. The former is to be expected, as we are talking about \( \mathbb{C}(t)\) which has inherent connections to complex analysis. The latter comes in because there is an analogue of Galois theory for covering spaces. One nice thing about this problem is that it directly translates the covering Galois theory to the vanilla field one for the context. This post will assume the prerequisites of Galois theory and some basic pointset topology. Some algebraic topology will be used, but the reader can safely blackbox those. I will explain briefly the concepts used and the reader wont need to know those beyond the details I provided for this blog.

Galois theory of covering spaces

First, we are going to develop the Galois theory for covering spaces. Covering spaces of \( X\) are maps \( p:Y\longrightarrow X\) such that around each point \( x\in X\) there is a neighborhood \( V\ni x\) such that \( p^{-1}(V)= \coprod U_i\) with the restrictions \( p: U_i\longrightarrow V\) is a homeomorphism. That is to say that there lies over this neighborhood in \(X\) disjoint copies of it in \(Y\) . The classic example of a covering space is the real number line covering the circle: the map \(\mathbb{R}\longrightarrow S^1\) defined by sending \(x\mapsto e^{2\pi i x}\) . This is demonstrated in figure 1.

Figure 1: The real number line covering the circle.

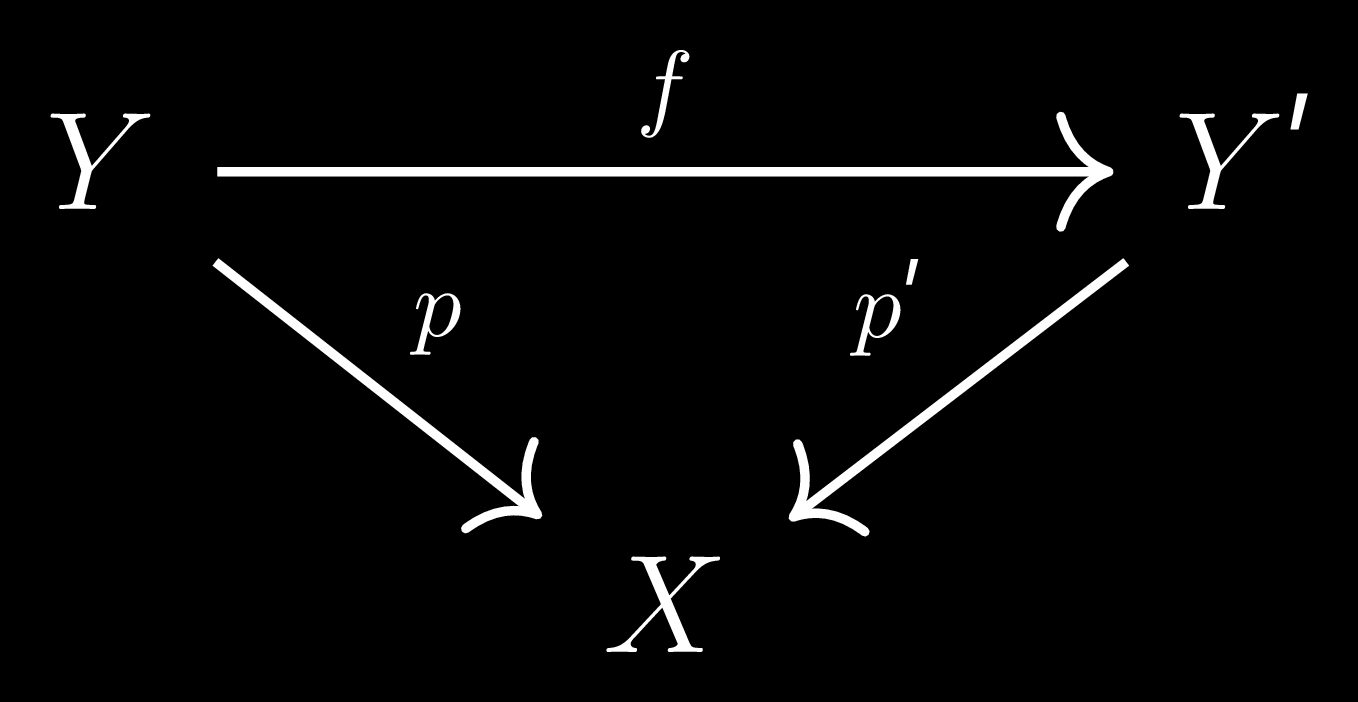
Now morphisms of covering spaces are as shown in the diagram below, defined this way as we care about the things that lie above a point and these preserve that. And then by \(\text{Aut}(Y|X)\) we will mean the automorphisms of \(Y\) as a covering space for \(X\) . By subcovers of \(p:Y\longrightarrow X\) we will mean covers \(p':Y'\longrightarrow X\) such that there is a morphism of covers \(f:Y\longrightarrow Y'\) which is also a covering map of \(Y'\) .Now for nice spaces (path connected,locally path connected and semi-locally simply connected spaces) there is a maximal connected cover (i.e every connected cover of \(X\) is covered by this). We call this the universal covering \(\tilde{X}\) of \(X\) .As an example the universal cover of the circle is the real number line. It turns out that this space is simply connected, and that \(\text{Aut}(\tilde{X}|X)\cong \pi_1(X)\) . The idea is that \(\pi_1(X)\) are all the loops in \(X\) , and if you lift the loop along a covering map, you get a path in \(\tilde{X}\) . Then take all the preimages of a point and lift a loop with the begining being a set point in the preimage, and then look at the endpoint of the lifted path.There is a unique automorphism that permutes the preimages like this(from begining of path to the end). The maximality of the universal cover would ensure that this map \(\pi_1(X,x) \longrightarrow \text{Aut}(Y|X)\) we just described by lifting loops is an isomorphism. For example lifting paths from the circle is like translation in the real number line, which would corrospond to the winding number of a circle. For all the details on why an universal cover exists and how to find its automorphism group, I refer the reader to chapter 1 of Hatcher's "algebraic topology".

Figure 2: Morphisms of covers

Now, it is clear that \(\text{Aut}(Y|X)\) acts on the fibres of a given point. This is much like how the galois group of a field extension acts on the set of roots of a polynomial. Now we like this extension when its a Galois extension, i.e the galois group acts transitively on the roots of a polynomial and the extension is seperable (latter is irrelevant to our case). So a natural way to define a galois covering is to require this deck action of \(\text{Aut}(Y|X)\) on the preimages of \(x\) to be transitive. Does this yield good theory? the answer is yes. Note that in particular the universal cover is a galois cover.

Suppose \(p:Y\longrightarrow X\) is a galois cover, then subgroups of \(\text{Aut}(Y|X)\) corrospond to subcovers of \(Y\) and normal subgroups to galois subcovers. The corrospondence is defined as follows: for a subcover \(Y'\) simply send it to the subgroup \(\text{Aut}(Y|Y')\) and for a subgroup \(H\) send it to the orbit space of \(Y\) with respect to the action of \(H\) (topologized with the quotient topology, this will be a subcover.). Notice that this is almost completely analogous to vanilla galois theory for fields. We send a subfield to a galois group and we send a subgroup to its fixed subfield. We also have, similar to vanilla Galois theory that \(\text{Aut}(Y'|X) \cong \text{Aut}(Y|X)/\text{Aut}(Y'|X)\) . I will leave proving all of this as an exercise for the reader.

Riemann surfaces and their function fields

A riemann surface is a topological space \(X\), together with a collection of charts (called an atlas)\(\phi_i:U_i \longrightarrow V_i\) where \(U_i\) is an open subset of \(X\) and \(V_i\) an open subset of \(\mathbb{C}\) with \(\phi_i\) being a homeomorphism. This is to say that our space locally looks like the complex plane. We require the addition condition that for two charts \(\phi_i\) and \(\phi_j\) we should be able to transition holomorphically. That is to say \(\phi_i\phi_j^{-1}\) is a holomorphic map (which makes sense as this is a map between subsets of \(\mathbb{C}\). This condition exists to allow us to define holomorphic maps of riemann surfaces, I.e say a map \(f:X\longrightarrow \mathbb{C}\) is holomorphic if for each point has a chart with \(f\phi_i^{-1}\) is holomorphic. The transition maps being holomorphic means that if we had another chart around a point, we could simply transition to a chosen one holomorphically and this property would be preserved. We can similarly define a holomorphic map between two surfaces \(f:X\longrightarrow Y\) to be a map such that \(\phi_{yj} f \phi_{xi}^{-1}\) is always holomorphic. So we have essentially defined these surfaces that we can do complex analysis on. Now we say that two atlases on \(X\) are compatible if their union is also an atlas (i.e you can holomorphically tansition between the two atlases). Because of this when we talk about a Riemann surfaces, we just assume it has a maximal atlas on it.

Figure 3: Transition map between two charts

Now as examples of Riemann surfaces, we have the complex plane, with a single chart just being the identity map. We also have the Riemann sphere \(\mathbb{CP}^1\) which topologically is the same as a 2-sphere. We make it a riemann surface by considering this as \(\mathbb{C}\cup \{\infty\}\) (we get this by stereographic projection, draw the sphere in 3d and take the xy plane. Then draw a line through the northpole and a selected point and see where it intersects the plane. Everything except the north pole gets mapped to the plane, and the northpole under this would in a sense "get mapped to infinity".), and then giving it two charts. one of them is simply the identity on the open subset \(\mathbb{C}\), and the other is the map \(z\mapsto \dfrac{1}{z}\) on everything but \(0\).

Now we can define meromorphic functions on a surface in the same way as holomorphic functions,i.e functions so that \(f\phi^{-1}\) is meromorphic for all charts(so they are holomorphic if you remove a discrete set called the poles.) Notice that the holomorphic functions on \(X\), \(\mathscr{O}(X)\) is a ring under function addition and multiplication. Now the Meromorphic functions \(\mathscr{M}(X)\) actually go a bit further, they form a field, as they are allowed to take on the value of infinity. Also notice that if we have a holomorphic map \(f:Y\longrightarrow X\), then we have an induced \(f^\star:\mathscr{M}(X) \longrightarrow \mathscr{M}(Y)\) defined by sending the meromorphic function \(h:X\longrightarrow \mathbb{CP}^1\) to \(hf:Y\longrightarrow \mathbb{CP}^1\). Now field homomorphisms are always injective, so this actually induces a field extension of \(\mathscr{M}(X)\).

Now we do a computation, for \(\mathscr{M}(\mathbb{CP}^1)\). Now since the Riemann sphere is compact, there are only finitely many poles for a meromorphic function (as the poles form a discrete set). So we can multiply by appropriate factors to get rid of the poles on the \(\mathbb{C}\) part, for example multiplying by \((x-1)^2\) would get rid of a pole of order \(2\) at \(x=1\). Now this meromorphic function restricted to the complex plane is holomorphic, and hence a power series. Notice that the power series now has to terminate, as otherwise the pole at infinity would not be finite. So this is really a polynomial, and since we multiplied by another polynomial to get to this form, our meromorphic function is a rational function. So \(\mathscr{M}(\mathbb{CP}^1)=\mathbb{C}(t)\). So to study field extensions of this field, we should study holomorphic maps into the Riemann sphere.

</section>

Holomorphic maps of compact surfaces are branched covering maps

If we have a map between Riemann surface, it locally looks like \(z\mapsto z^k\) for some k, the ramification index of \(z\).What this means is that for each holomorphic map \(f:Y\longrightarrow X\) and each point \(z\in Y\), we can find charts such that \(\psi f\phi^{-1}=z^k\). I refer the reader to Forster's "lecture on Riemann surfaces" theorem 2.1 for the proof.This implies the open mapping theorem, that holomorphic maps send open sets to open sets. Now notice that whenever \(k=1\) we have a local homeomorphism around that point, as \(f\) would be injective and open mapping theorem means the local inverse would be too.

Now suppose we have a map \(f:Y\longrightarrow X\) is of compact riemann surfaces. Now consider the set of unramified points (points with \(k\geq 2\)) \(A\), then \(A\) is discrete. This is because the map locally looks like \(z^k\) and we can always take a small neighborhood not containing \(0\) on which this is a local homeomorphism. So we have a finite number of unramified points for maps between compact surfaces. Now the open mapping theorem gives us that whenever \(X\) is connected, \(f\) is surjective. This is because the image of \(Y\) would be both open and compact(and hence closed), and connected spaces only have trivial clopen sets. So now for each unramified point \(x\in X\), let \(y_i\) be the preimages, and then pick a neighborhood \(U\ni x\) and neighborhoods \(V_i\ni y_i\) with \(f:V_i \longrightarrow U\) a homeomorphism (we can do this because local homeomorphism). We can pick the \(V_i\) to be all disjoint and then \(f^{-1}(U)=\cup_i V_i\). So if we remove the ramified points we actually have a covering map.

We showed that holomorphic maps between compact surfaces are branched coverings, now we show the converse. If \(X\) is a Riemann surface, and \(f:Y\longrightarrow X\) a covering map, then we can pull back the charts on X onto Y (i.e \(\phi_i f\) on Y are the charts) and then by construction this makes \(f\) into a holomorphic map. So now we have a direct analogy between the two galois theories, we have the galois theory of coverings from holomorphic maps(as these are almost covering maps) and the field extension of the meromorphic fields induced by these maps.

The covering Automorphism group is the same as the Galois group

Lets say we have a covering map \(f':Y'\longrightarrow X'\) where \(X'\) is \(X\) with a finite set of (unramified) points removed, we can uniquely extend this to a branched cover (and hence a holomorphic map) of \(X\). See Forster theorem 8.4 for proof, and then theorem 8.5 to see that covering morphisms of \(Y'\) and \(Z'\) over \(X'\) extend uniquely to that of holomorphic maps between \(Y\) and \(Z\) (these are the unique spaces where the covering maps extend to) over \(X\). Notice the latter means each morphism of \(Y'\) to \(Z'\) induces a field homomorphism from \(\mathscr{M}(Z)\)to \()\mathscr{M}(Y)\) that fixed \(\mathscr{M}(X)\). In particular we have a morphism \(\text{Aut}(Y'|X')\longrightarrow \text{Gal}(Y|X)\). Now if the covering is galois then this is injective as different holomorphic maps induce different field automorphims. Now if the galois covering was of degree n, then its automorphism group is of order n(how one point is sent to another uniquely determines a cover automorphism). To show surjectivity, we want to show that the galois groups for the field extension also has order n.

So first suppose we have a meromorphic function \(h\in\mathscr{M}(Y)\). Take a point \(x\in X'\) and a neighborhood \(U\ni x\) with \(f^{-1}(U) = \cup V_i\), with the \(V_i\) disjoint, so that \(f: V_i\longrightarrow U\) are homeomorphisms. Now call the inverse \(s_i:U\longrightarrow V_i\), and \(h_i = h s_i\) meromorphic functions on \(U\). Now take the symmetric polynomials \(a_k\) in the \(h_i\), and \(\prod(t-h_i)\) which has the symmetric polynomials as coefficients, then these are also meromorphic functions on \(U\). Now if we do this for all points \(x\in X'\) and glue the symmetric polynomials together (as on intersection of two such open sets they have to agree) we get global functions \(a_k\) on \(X\), and hence a Global polynomial with the coefficients \(a_k\). Now \(h\) satisfies this polynomial as its restriction to one of these \(U\)s is \(\prod(h-h_if)=0\), and then we glue it together to get its \(0\) globally on \(Y'\). Note that we used \(h_i f\) as the field extension is really \(\mathscr{M}(Y)|f^\star \mathscr{M}(X)\). This means all meromorphic functions on Y satisfy an irreducible polynomial of degree less than n over \(f^\star\mathscr{M}(X)\). Finally we use Riemann's existence theorem, which garuntees a function \(h\in\mathscr{M}(Y)\) which would seperate the \(y_i\) lying over a given \(x\),which means that the polynomial has to have degree n. For proof of Riemann's existence theorem, I refer the reader to Forster's chapter 2 which uses sheaf cohomology to prove it. Now \(\mathscr{M}(X)(h) = \mathscr{M}(Y)\). This is because if we had another \(g\in \mathscr{M}(Y)\) then \(\mathscr{M}(X)(h)\subset \mathscr{M}(X)(h,g)= \mathscr{M}(X)(k) \) by primitive element theorem, and since \(k\) has degree atmost n, we have the equality \(\mathscr{M}(X)(h) = \mathscr{M}(X)(k)\) and so \(g\in \mathscr{M}(X)(h)). This proves the galois group has order n and hence that the covering automorphism group is the same thing as the galois group.

Combining all the ideas

Start with a group \(G\) generated by \(n\) elements. Take Riemann sphere with \(n+1\) points removed. This is homotopy equivalent to the wedge of \(n\) circles so its \(\pi_1\) is the free group on \(n\) elements. So this is the automorphism group of this spaces universal cover. Now we can take a subcover \(Y\) whose automorphism group is \(G\) by the galois theory of covering. We know by the last section that this induces an extension \(\mathscr{M}(Y)|\mathbb{C}(t)\) whose galois group is \(G\). We are done \(_\square\)

</section>

Updated:

Comments